หากกล่าวถึงคณิตศาสตร์ ทุกคนคงคิดว่าเป็น "ศาสตร์ที่ว่าด้วยเรื่องตัวเลข" ซึ่งอันที่จริงแล้วคำจำกัดความนี้เป็นเพียงคำจำกัดความดั่งเดิมของคณิตศาสตร์เท่านั้น ปัจจุบันคณิตศาสตร์ได้ถูกพัฒนาจนไม่สามารถใช้คำจำกัดความดังกล่าวได้อีกต่อไป ซึ่งหากผู้ที่สนใจอยากรู้ว่าคณิตศาสตร์มีประวัติความเป็นมาอย่างไร มีอะไรมากไปกว่าตัวเลข ก็คงบอกได้แต่เพียงว่า ต้องติดตามกันต่อไป อย่างไรก็ตาม คำจำกัดความนี้สามารถชี้ให้เห็นถึงรากฐาน และที่มาของคณิตศาสตร์ได้อย่างชัดเจน นั่นก็คือ ตัวเลข นั่นเอง
คณิตศาสตร์เริ่มจากเป็นเกร็ดความรู้ที่มนุษย์นำมาใช้ให้เป็นประโยชน์ในการดำรงชีวิตในสมัยสี่พันปีก่อนค่อยๆ มีกฎเกณฑ์ทวีเพิ่มพูนขึ้นตลอดมา คณิตศาสตร์เปรียบเหมือนต้นไม้ นับวันจะผลิดอกออกผลนำประโยชน์มาให้มนุษยชาติ มนุษย์ทุกยุคทุกสมัยสนใจวิชาคณิตศาสตร์ การให้ความรู้ทางคณิตศาสตร์แก่เยาวชนของชาติ จึงมีความสำคัญอย่างมาก
ระบบจำนวนจึงเป็นเรื่องของธรรมชาติที่มนุษย์ต้องการใช้ในการนับจำนวน เพื่อจะได้ทราบปริมาณ และเปรียบเทียบค่า หรือใช้ประโยชน์ในชีวิตประจำวันได้มากมายมหาศาล
ความเป็นอยู่ของผู้คนเกี่ยวข้องกับการทำการเกษตร การเพาะปลูก เมื่อดำเนินการตั้งถิ่นที่อยู่อาศัย ก็ต้องมีการคำนวณพื้นที่ มีการเรียนรู้เรื่องเวลาและฤดูกาล เมื่อเพาะปลูกได้ก็ต้องรับรู้ปริมาณผลผลิตที่ได้รับ จึงมีการตวงข้าวสาลี ข้าวบาเลย์ และเป็นที่มาของมาตราต่าง ๆ ที่ใช้ ชีวิตความเป็นอยู่ของชนทุกชาติจะคุ้นเคยกับหน่วยปริมาณ และมาตราวัดที่แตกต่างกันออกไป
ชาวไทยคุ้นเคยกับมาตราวัดระยะทางแบบ คืบ ศอก วา เส้น มาก่อน ทำให้หน่วยวัดพื้นที่เป็นไร่ เป็นงาน อย่างไรก็ดีหน่วยวัดปริมาตรของไทยที่คุ้นเคยเดิมคือเป็นถัง เกวียน หรือแม้แต่การแบ่งเวลาก็มีการแบ่งเป็นโมง เป็นยาม
ในแต่ละชาติ แต่ละภาษาจึงมีมาตรฐานปริมาณของตนเอง มีหน่วยเงินตรา หรือหน่วยใช้ในชีวิตประจำวันต่าง ๆ ที่แตกต่างกัน แต่เมื่อมีการคบค้าสมาคมกันระหว่างประเทศ มีการค้าขายแลกเปลี่ยน ทำให้การดำเนินชีวิตที่ต้องมีมาตรฐานกลาง หรือหน่วยวัดกลางและเป็นที่ยอมรับกันทั่วโลก
แน่นอนทีเดียวที่แต่ละประเทศย่อมมีสัญลักษณ์แทนตัวเลขที่แตกต่างกันไป จึงขอเริ่มต้นประวัติศาสตร์ของคณิตศาสตร์ด้วยตัวเลขที่แต่ละอารยะธรรมคิดค้นขึ้นแต่ละยุคสมัย
ความคิดทางคณิตศาสตร์ยุคตอนต้น
สมัยอียิปต์โบราณ (Civilization of Ancient Egypt)
|
อียิปต์โบราณ หรือ ไอยคุปต์ เป็นหนึ่งในอารยธรรมที่เก่าแก่ที่สุดในโลก ตั้งอยู่ทางตอนตะวันออกเฉียงเหนือของทวีปแอฟริกา มีพื้นที่ตั้งแต่ตอนกลางจนถึงปากแม่น้ำไนล์ ปัจจุบันเป็นที่ตั้งของประเทศอียิปต์ อารยธรรมอียิปต์โบราณเริ่มขึ้นประมาณ 3,150 ปีก่อนคริสต์ศักราช โดยการรวมอำนาจทางการเมืองของอียิปต์ตอนเหนือและตอนใต้ ภายใต้ฟาโรห์องค์แรกแห่งอียิปต์ และมีการพัฒนาอารยธรรมเรื่อยมากว่า 3,000 ปี ประวัติของอียิปต์โบราณปรากฏขึ้นในช่วงระยะเวลาหนึ่ง หรือที่รู้จักกันว่า "ราชอาณาจักร" มีการแบ่งยุคสมัยของอียิปต์โบราณเป็นราชอาณาจักร ส่วนมากแบ่งตามราชวงศ์ที่ขึ้นมาปกครอง จนกระทั่งราชอาณาจักรสุดท้าย หรือที่รู้จักกันในชื่อว่า "ราชอาณาจักรใหม่" อารยธรรมอียิปต์อยู่ในช่วงที่มีการพัฒนาที่น้อยมาก และส่วนมากลดลง ซึ่งเป็นเวลาเดียวกันที่อียิปต์พ่ายแพ้ต่อการทำสงครามจากอำนาจของชาติอื่น จนกระทั่งเมื่อ 31 ปีก่อนคริสต์ศักราชก็เป็นการสิ้นสุดอารยธรรมอียิปต์โบราณลง เมื่อจักรวรรดิโรมันสามารถเอาชนะอียิปต์ และจัดอียิปต์เป็นเพียงจังหวัดหนึ่งในจักรวรรดิโรมัน
อารยธรรมอียิปต์พัฒนาการมาจากสภาพของลุ่มแม่น้ำไนล์ การควบคุมระบบชลประทาน, การควบคุมการผลิตพืชผลทางการเกษตร พร้อมกับพัฒนาอารยธรรมทางสังคม และวัฒนธรรม พื้นที่ของอียิปต์นั้นล้อมรอบด้วยทะเลทรายเสมือนปราการป้องกันการรุกรานจากศัตรูภายนอก นอกจากนี้ยังมีการทำเหมืองแร่ และอียิปต์ยังเป็นชนชาติแรกๆที่มีการพัฒนาการด้วยการเขียน ประดิษฐ์ตัวอักษรขึ้นใช้ ,การบริหารอียิปต์เน้นไปทางสิ่งปลูกสร้าง และการเกษตรกรรม พร้อมกันนั้นก็มีการพัฒนาการทางทหารของอียิปต์ที่เสริมสร้างความแข็งแกร่งแก่ราชอาณาจักร โดยประชาชนจะให้ความเคารพกษัตริย์หรือฟาโรห์เสมือนหนึ่งเทพเจ้า ทำให้การบริหารราชการบ้านเมืองและการควบคุมอำนาจนั้นทำได้อย่างมีประสิทธิภาพ
ชาวอียิปต์โบราณไม่ได้เป็นเพียงแต่นักเกษตรกรรม และนักสร้างสรรค์อารยธรรมเท่านั้น แต่ยังเป็นนักคิด, นักปรัชญา ได้มาซึ่งความรู้ในศาสตร์ต่างๆมากมายตลอดการพัฒนาอารยธรรมกว่า 3,000 ปี ทั้งในด้านคณิตศาสตร์, เทคนิคการสร้างพีระมิด, วัด, โอเบลิสก์, ตัวอักษร และเทคนิคโลยีด้านกระจก นอกจากนี้ยังมีการพัฒนาประสิทธิภาพทางด้านการแพทย์, ระบบชลประทานและการเกษตรกรรม อียิปต์ทิ้งมรดกสุดท้ายแก่อนุชนรุ่นหลังไว้คือศิลปะ และสถาปัตยกรรม ซึ่งถูกคัดลอกนำไปใช้ทั่วโลก อนุสรณ์สถานที่ต่างๆในอียิปต์ต่างดึงดูดนักท่องเที่ยว นักประพันธ์กว่าหลายศตวรรษที่ผ่านมา ปัจจุบันมีการค้นพบวัตถุใหม่ๆในอียิปต์มากมายซึ่งกำลังตรวจสอบถึงประวัติความเป็นมา เพื่อเป็นหลักฐานให้แก่อารยธรรมอียิปต์ และเป็นหลักฐานแก่อารยธรรมของโลกต่อไป
ในสมัยโบราณ อียิปต์เป็นชาติที่เจริญรุ่งเรืองทางด้านศิลปวิทยาการก่อนชาติอื่นๆ ชาวอียิปต์รู้จักบันทึกจำนวนโดยใช้สัญลักษณ์ต่างๆ โดยการเขียนสัญลักษณ์แทนจำนวนของชาวอียิปต์ ใช้วิธีรวมค่าของสัญลักษณ์เหล่านั้น จะไม่คำนึงถึงตำแหน่งของสัญลักษณ์ ดังนั้น จำนวนเดียวกันอาจจะเขียนสัญลักษณ์สลับที่เป็นแบบต่างๆ ได้
.jpg)
อียิปต์โบราณ มีอาณาเขตครอบคลุมที่ราบลุ่มแม่น้ำไนล์จากเมืองแอสวาน (Aswan) จนจรดชายฝั่งทะเลเมดิเตอร์เรนียนของประเทศอียิปต์ อียิปต์โบราณเป็นอารยธรรมหนึ่งที่เก่าแก่ที่สุดในโลก และเป็นอารยธรรมแรกที่ส่งเสริมวิทยาศาสตร์ ชาวอียิปต์โบราณให้ความสำคัญอย่างมากกับการจดบันทึก และการสื่อสารจึงได้ประดิษฐ์กระดาษปาปิรุส (papyrus) ขึ้น ที่มีอายุ 3,850 ปี กระดาษปาปิรุสทำมาจากต้นกกที่เติบโตอย่างแพร่หลายในแถบลุ่มแม่น้ำไนล์
ในพีระมิดได้แสดงให้เรา ณ วันนี้เห็นว่า ชาวอียิปต์รู้จักเลขเศษส่วน รู้วิธีแบ่งขนมปังในอัตราส่วนต่างๆ รู้วิธีหาพื้นที่ของสามเหลี่ยม รู้วิธีหาปริมาตรของทรงกระบอก เมื่อมีการกำหนดความยาวเส้นผ่าศูนย์กลาง และส่วนสูงของทรงกระบอกมาให้ นอกจากนี้นักคณิตศาสตร์อียิปต์ยังได้พบว่าอัตราส่วนระหว่างความยาวของเส้นรอบวง/เส้นผ่าศูนย์กลางของวงกลมใดๆ มีค่า 256/81 หรือ 3.16
ชาวอียิปต์โบราณสื่อความหมายด้วยอักษรภาพที่เรียกว่า ไฮโรกลิฟ (Hieroglyph) ซึ่งรวมไปถึงตัวเลขด้วย อักษรภาพแทนตัวเลขต่างๆ มีดังนี้
ยุคบาบิโลน (Babylon)
บาบิโลนเป็นนครของชาวเซไมท์กลุ่มหนึ่ง อยู่ทางภาคใต้ของบริเวณเมโสโปเตเมีย เมื่อประมาณ 2,350 ก่อน คริสต์ศักราช ซึ่งพัฒนาต่อๆมาเป็นนครใหญ่และสวยงามมากแห่งหนึ่งของโลก มีกำแพงเมืองล้อมรอบตัวเมืองเป็นระยะทางเกือบ 8 กิโลเมตร มีหอคอยกั้นระหว่างกำแพงเป็นระยะๆ มีประตูเมือง 8 แห่ง เข้าสู่ภายในเมือง ตัวอาคารสร้างด้วยอิฐ ตรงประตูเมืองวาดภาพเป็นรูปสัตว์นับร้อยๆ ภาพ ตกแต่งสวยงาม มีถนนบนกำแพงเมืองกว้างพอให้ทหารเดินไปรอบๆเมือง เพื่อป้องกันข้าศึก
ชาวกรีกได้บันทึกไว้ว่ากำแพงเมืองบาบิโลนสูง 700 ฟุต มีความหนามาก จนส่วนบนของกำแพงกว้างพอให้รถศึกเทียมด้วยม้า4ตัว วิ่งไปบนส่วนของกำแพงได้ แต่ข้อมูลนี้ถูกโต้แย้งในเรื่องของความสูงว่าจริงๆ แล้วอาจบันทึกผิด น่าจะสูงแค่ 70 เมตร
อารยธรรมยิ่งใหญ่ของบาบิโลนที่ทิ้งไว้ให้แก่มนุษยชาติ สำคัญๆได้แก่ กฏหมายของบาลิโลนที่มีความยุติธรรมและเขียนจารึกไว้บนแผ่นดินเหนียวซึ่งยังคงเหลือมาถึงทุกวันนี้ โดยกษัตริย์ฮัมมุรัมบี ตรากฏหมายเรื่องต่างๆ เช่น การสมรส โจรกรรม หนี้สิน การจราจรทางน้ำ ค่าจ้างแรงงาน การรักษาคลอง กฏหมายกำหนดราคา ฯลฯ เหล่านี้เป็นกฏหมายที่ยุติธรรมแต่บทลงโทษโหดเ้ยม ซึ่งเป็นจุดเริ่มต้นของกฏหมายที่ดี จนกระทั่งโรมันนำมาใช้ทั่วจักรวรรดิโรมัน และประเทศยุโรปยังเอากฎหมายโรมันมาใช้อยู่ในปัจจุบัน
บาบิโลนและอัสซีเรีย 2 จักรวรรดิของชาวเซไมท์ในเมโสโปเตเมียดินแดนแห่งลุ่มน้ำไทกรีส ยูเฟรตีส ได้เจริญรุ่งเรืองอยู่ช่วงเวลาหนึ่ง และทิ้งอารยธรรมไว้แก่โลกก่อนที่จะถูกมหาอำนาจใหม่ในตะวันออกกลาง คือ เปอร์เซีย ได้ทำลายทั้งอัสซีเรีย(ปี 612 ก่อน ค.ศ.) และบาบิโลน (ปี 539 ก่อน ค.ศ.)
ชาวบาบิโลน (ประเทศอิรักในปัจจุบัน) และชาวอียิปต์รู้จักเขียนสัญลักษณ์แทนจำนวน รู้จักเลข เศษส่วน รู้จักใช้ลูกคิดบวก ลบ คูณ หารตัวเลข ความรู้เกี่ยวกับจำนวนได้นำมาใช้ในการติดต่อค้าขาย การเก็บภาษี การรู้จักทำปฏิทิน และการรู้จักใช้มาตรฐานเกี่ยวกับเวลา เช่น 1 ปีมี 365 วัน 1 วันมี 24 ชั่วโมง 1 ชั่วโมงมี 60 นาที 1 นาทีมี 60 วินาที ความรู้ทางเรขาคณิต เช่น การวัดระยะทาง การวัดมุม นำมาใช้ในการก่อสร้างและการรังวัดที่ดิน เขาสนใจคณิตศาสตร์ในด้านนำไปใช้ให้เป็นประโยชน์ได้เท่านั้น
จากหลักฐานทางคณิตศาสตร์ที่เก่าแก่ที่สุดของอารยธรรมมนุษย์ในยุคบาบิโลน ซึ่งอยู่ในช่วงเวลาประมาณห้าพันปีที่แล้ว ชาวบาบิโลนมีอารยธรรมที่เก่าแก่อยู่แถบลุ่มแม่น้ำยูเฟรติส ได้ใช้ตัวเลขการนับด้วยฐานหกสิบ และแบ่งหน่วยเวลาเป็นมาตรา 60 ดังที่เราใช้กันมาในเรื่องเวลา และใช้แบ่งวงกลมเป็นองศา ฟิลิปดา เป็นต้น
ตัวเลขแทนเวลาจะเขียนได้เป็น 5h 25' 30" มีความหมายว่า 5ชั่วโมง 25 นาที 30 วินาที หรือเขียนในฐาน 60 เป็น 5 25/60 30/3600 ซึ่งถ้าเขียนเป็นตัวเลขฐานสิบจะได้ 5 4/10 2/100 5/1000
ชีวิตความเป็นอยู่ของคนเกี่ยวข้องกับการนับและปริมาณ หน่วยนับจึงมีความสำคัญ เพราะการสื่อสารเพื่อจะบอกปริมาณระหว่างกันจำเป็นต้องมีหน่วยนับ ลองจินตนาการดูว่ามนุษย์ชาวบาบิโลเนียยังไม่รู้จักกับตัวเลขทศนิยม รู้จักแต่จำนวนเต็ม และมีฐานหกสิบ หลักฐานที่สำคัญที่ยืนยันว่าชาวบาบิโลเนียใช้เลขฐานหกสิบ ก็คือมีการค้นพบตารางคำนวณที่ลุ่มน้ำยูเฟรติสในปี ค.ศ. 1854 ตารางที่พบเป็นตารางตัวเลขยกกำลังสอง เช่น 82 = 1 4 ซึ่งมีความหมายเป็น 82 = 1 4 = 1 x 60 + 4 = 64 หรือตัวอย่าง 592 = 58 1 (=58 x 60 + 1 = 3481)
สิ่งที่น่าประหลาดใจคือ ชาวบาบิโลเนียรู้จักวิธีการคูณและหารตัวเลขแล้ว แต่การคูณและหารตัวเลขยังมีลักษณะที่ใช้ตารางยกกำลังสองของตัวเลขที่ทำขึ้น โดยสมมุติว่า ต้องการคูณตัวเลข aและ b
ชาวบาบิโลเนียใช้หลักการของการยกกำลังสองของตัวเลขที่ได้จากตาราง โดยใช้หลักการ
a.b = ((a+b)2-a2-b2)/2
|
จากหลักการนี้เขียนได้ -->
|
a.b = (a+b)2/4 - (a-b)2/4
|
เช่น ถ้าต้องการผลลัพธ์ของ 5.3 จะได้ (64/4) - 4/4 = 15
ลองจินตนาการดูว่าชีวิตความเป็นอยู่ของชาวบาบิโลเนียที่เกี่ยวข้องกับเลขฐานหกสิบ แม้แต่หน่วยเงินก็เป็น 60 และแบ่งย่อยเป็นหกสิบ แต่หากแบ่งส่วนย่อยบางส่วนลงไป เช่น 1/13 ซึ่งมีค่าเท่ากับ 7/91ซึ่งถ้าคิดโดยประมาณก็จะเป็น 7/90
ข้อสังเกต ตัวเลขบาบิโลน เป็นตัวเลขในระบบฐานหกสิบ เมื่อนำสัญลักษณ์ตัวเดิมไปวางไว้ในตำแหน่งหรือหลักที่ต่างกัน จะได้ค่าต่างกัน เนื่องจากชาวบ้านบาบิโลนยังไม่รู้จักใช้สัญลักษณ์ศูนย์ จึงมีข้อยุ่งยากของการใช้ตัวเลขในระบบนี้ คือถ้าจำนวนในหลักใดขาดหายไป จะทำให้เกิดความสับสนในการอ่านและการเขียน
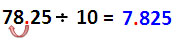
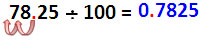
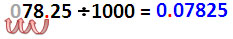
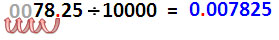
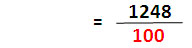
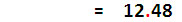
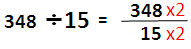
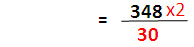
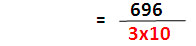
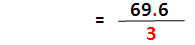










.jpg)

